National Institute of Standards and Technology

Computational Chemistry Comparison and Benchmark DataBase
Release 22	May 2022
NIST Standard Reference Database 101

I	Introduction
II	Experimental data
III	Calculated data
IV	Data comparisons
V	Cost comparisons
VI	Input and output files
VII	Tutorials and Units
VIII	Links to other sites
IX	Feedback
X	Older CCCBDB versions
XII	Geometries
XIII	Vibrations
XIV	Reaction data
XV	Entropy data
XVI	Bibliographic data
XVII	Ion data
XVIII	Bad calculations
XIX	Index of properties
XX	H-bond dimers
XXI	Oddities

---

NIST policy on privacy, security, and accessibility.

---

© 2013 copyright by the U.S. Secretary of Commerce on behalf of the United States of America. All rights reserved.

The National Institute of Standards and Technology (NIST) is an agency of the U.S. Department of Commerce.

Please send questions, comments, corrections, additions and suggestions to cccbdb@nist.gov.

VII.C.11.

Tutorial on Electric Quadrupole Moments

What is it?

Any distribution of charges can be described using a multipole expansion. The multipole expansion breaks the distribution down into the total charge, the dipole, the quadrupole, the octapole, etc.

Formulas

(I'm still working on this page) see for example: http://en.wikipedia.org/wiki/Electric_Quadrupole

Pictures

Practical considerations

Molecular electric quadrupole moments in general are derived (sometimes it seems in rather involved ways) from some other measured property. They are derived from the measurement of the second virial coefficient of gases (a measure of how non-ideal a gas is) and spectroscopic observations changes in the rotational energy levels when the molecule is in a magnetic or electric field. In both cases the quadrupole moment is a fudge factor that tweaks some other property. There is a physical basis for the expansion used in both cases, but I would not expect the values obtained from two such different measurements, with different random and systematic errors, to agree within the stated uncertainties of each measurement.

Primitive? Traceless?

Some of the confusion over factors of two, and "primitive" versus "traceless" comes from this use of the quadrupole moment as a coefficient in different expansions describing different properties. The electric quadrupole moment can be described as a 3x3 symmetric matrix with components:

Qxx	Qxy	Qxz
Qxy	Qyy	Qyz
Qxz	Qyz	Qzz

This has 6 different values. However, the traceless version is used to omit the spherical component. An experimental measurement will observe the part of the quadrupole that is different from spherical. Just to make it a little more confusing instead of just subtracting the trace the diagonal elements of the "traceless" matrix are defined as:
xx' = (3*xx-trace)/2
yy' = (3*yy-trace)/2
zz' = (3*zz-trace)/2
I believe this comes from the use of the components in particular equations.

One reference that discusses how the "gas-property people" use the quadrupole is in: "Theory of Molecular Fluids Volume1: Fundamentals" C.G. Gray and K.E. Gubbins, Oxford University Press, New York, 1984

Relation between cartesian and spherical components

monopole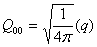
dipole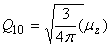
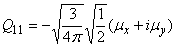quadrupole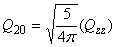

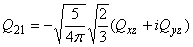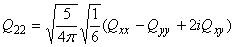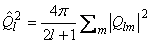
However one often wants just the magnitude of the quadrupole, where the magnitude of a general multipole moment is defined as:

The previous equations are from "Theory of Molecular Fluids Volume1: Fundamentals" C.G. Gray and K.E. Gubbins, Oxford University Press, New York, 1984