Computational Chemistry Comparison and Benchmark DataBase Release 22 (May 2022) Standard Reference Database 101 National Institute of Standards and Technology
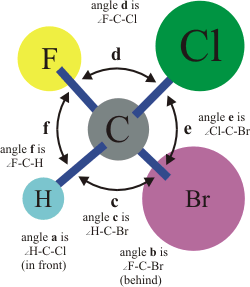
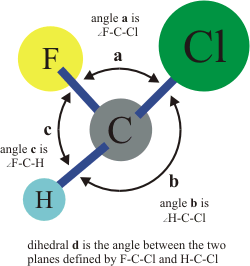
	Home All data for one species Geometry Experimental Experimental Geometries Same bond/angle many molecules Internal Coordinates by type Bond angles Calculated Calculated geometry Rotational constant Moments of inertia Products of moments of inertia BSE Bond lengths Show me a calculated geometry Comparisons Bonds, angles Rotational Constants Products of moments of inertia Point group Bad Calculations Bad moment of inertia Tutorials and Explanations Angle formulas Vibrations Experimental Vibrational frequencies Calculated Frequencies Scale factors Reactions Entropies Ions List Ions Energy Calculated Ionization Energy Compare Ionzation energy Electron Affinity Calculated Electron affinity Compare Electron affinity Proton Affinity Calculated Proton affinity Compare Proton affinity Ionization changes point group Experimental One molecule all properties One property a few molecules Enthalpy of formation Entropy Integrated Heat Capacity Heat Capacity Rotational Constants Vibrational Frequencies Dipole moment Ionization Energy Polarizability Quadrupole Point Groups Geometry Experimental Geometries Internal Coordinates by type Bond angles Rotational Constants Point Groups Diatomic bond lengths Vibrations Vibrational frequencies Diatomic Triatomics Energy Atomization Energy Internal Rotation Electrostatics Dipole Quadrupole Polarizability Reference Data Reference states Spin Splittings Molecules with good enthalpy Enthalpy at 0 Kelvin Calculated Energy Optimized Energy Energy 298K Minimum conformation Hydrogen bonds H bond with counterpoise Reaction Reaction Energy 0K Reaction Energy 298K Internal Rotation Barriers to internal rotation Rotational barrier and dipole Rotational Barrier 2 molecules Orbital HOMO LUMO gap HOMO Orbital Energies Nuclear repulsion energy Correlation Full vs Frozen core energies Partial correlation energies Ion Calculated Ionization Energy Vertical ionization Energy Calculated Electron affinity Calculated Proton affinity Atom charge differences Excited State Singlet triplet gap Electronic state Transition state Basis Set Extrapolation BSE energy BSE Bond lengths Geometry Calculated geometry AIM bond orders One type of bond Rotation Rotational constant Products of moments of inertia Moments of inertia Inertial defects Second moments Point group State symmetry <r2> Sorted by r2 Z-matrix Bad Calculations Bad moment of inertia Bad Calculated Bond Lengths Bad point group Worst molecules Vibrations Frequencies Animated vibrations Anharmonic Zero point energy (ZPE) Scale Factors Scale factors Scale factor uncertainty Calculate a scale factor Why scale vibrations Set scaling factors Bad Calculations Bad Vib. HF vs MP2 Bad vib. Calc. vs exp. Big anharmonicity Electrostatics Charges Mulliken CHELP Aim ESP Dipole Dipole Dipole angle Dipole calculation types Quadrupole Polarizability Spin Spin density Entropy and Heat Capacity Entropy Reaction entropy Heat Capacity Reaction Reaction Energy 0K Reaction Energy 298K Isodesmic reactions Transition State Transition state Transition state frequencies Transition state geometries IRC Lookup by property By frequency Comparisons Geometry Bonds, angles Bond, angle, or dihedral DFT grid size on point group DFT grid on bond length Core correlation - bond length Same bond/angle many molecules Isoelectronic diatomics Isoelectronic triatomic angles Average bond lengths Rotation Rotational Constants Products of moments of inertia Point group Vibrations Vibrations 2 calculations Frequency differences One frequency Zero point energy Intensity Intensity for one mode Vibrational intensities Reduced mass comparison Anharmonic Triatomic Scale factors Energy Reaction Reaction Energy 0K Reaction Energy 298K Atomization 0K Atomization 298K Single point vs optimized DFT grid size on energy Semiempirical enthalpy Internal rotation Similar molecules Conformation Sets of isomers Sets of tautomers Isomers Entropy Entropy Heat capacity Entropy of several molecules Integrated heat capacity Reaction entropy Electrostatics Dipole Polarizability Several molecules Quadrupole Ion Compare Ionzation energy Koopman ionization energy Koopman IE for a few molecules Compare Electron affinity Compare Proton affinity Protonation Site Resources Info on Results Calculations Done Method and basis set List molecules One molecule Multiple conformers, states Multiple conformers, states Basis functions used I/O files Input/output files MOL file Z-matrix wfn files Glossary Conversion Forms B to I, I to B Angle formulas Integrated heat Capacity Calculating Enthalpy Links NIST Links NIST webbook bibliographic data CCCBDB Experimental data External links Basis Set Exchange Computational Chemistry List Thermochemistry in Gaussian Minnesota Database Collection Benchmark Energy and Geometry Point Groups Thermochemistry Thermochemistry Molecules with good enthalpy A → B + C Reference states Tutorials Vibrations Why scale vibrations Zero-point energies Entropy Methyl rotor entropy Entropy and conformations Energy Getting enthalpy of formation Vertical vs adiabatic IE Thermo from calculations Electrostatics Dipole parts by point group Quadrupoles Geometry Angle formulas Cost Cost Comparison Timings Comparison Bad Calculations Geometry Bad moment of inertia Bad Calculated Bond Lengths Bad point group Worst molecules Vibrations Bad vib. Calc. vs exp. Bad Vib. HF vs MP2 Bad scale factors Low excited states Oddities NaCN Is not linear FAQ Help Units Choose Units Energy Bond length Rotational Constant Moment of Inertia Dipole and Quadrupole Polarizability Explanations Hartree cm-1 Debye Credits Just show me Show me a calculated geometry Summary Using older interface Limit Basis sets Method options List Recent molecules Choose a few Molecules Number of atoms By heavy atoms Diatomics InChI Deuterated Dimers Geometry Point group Point group count Bonds types Isodesmic reactions Bad point group Multiple conformers, states Vibrations Big anharmonicity Energy Enthalpy at 0 Kelvin Similar molecules Similar Isomers Cis/trans Tautomers Multiple conformers, states Ions, Dipoles, etc. List Ions Ionization changes point group Dipole Quadrupole Polarizability Proton Affinities Index of CCCBDB Feedback Error form Wants
You are here: Home > Geometry > Tutorials and Explanations > Angle formulas OR Resources > Conversion Forms > Angle formulas OR Resources > Tutorials > Geometry > Angle formulas

Notes on converting between angles in tetravalent centers

C_3V molecules

In a C3v molecule such as CH3F, the angles FCH and HCH are related by symmetry. The angles a (FCH) and b (HCH) are related using the following formulas: Please note that the latter solution is not unique, and that solving for angle a may return 180° - a enter an angle greater than 0 and less than 180 a= Click to solve for b enter an angle greater than 0 and less than 120 b= Click to solve for a Click to clear

C_2V pentatomic molecules

In a C2V molecule such as CH2F2 the angle HCF can be related to the two angles HCH and FCF by symmetry. The angle e (HCF) is related to the angles c (HCH) and d (FCF) by: Please note that the latter solution is not unique, and that solving for angle e may return 180° - e enter two angles between 0 and 180 degrees c= d= e= Solve for angle c Solve for angle d Solve for angle e Clear

C_s tetravalent molecules

We use fluorochloromethane as an example. We know: angle c (H-C-H) (there is only one) angle d (F-C-Cl) (there is only one) angle e (H-C-Cl) (there are two equivilant) We want angle f (F-C-H) (there are two equivilant)

Arbitrary tetravalent center

In a arbitrary tetravalent center their are six angles. We define these angles as: a is angle H-C-Cl b is angle F-C-Br c is angle H-C-Br d is angle F-C-Cl e is angle Cl-C-Br f is angle H-C-F Assume we want angle f as a function of the other five angles. We can work with the cosines of the angles: ca = cos(a), cb = cos(b),etc. Define p and q: p = sqrt( (ca2 + cc2 + ce2 - 2*ca*cc*ce - 1) * ((ca2 + cb2 + cd2 - 2*ca*cb*cd - 1) ) q = ca*(cb*ce + cc*cd) - cb*cc - cd*ce The two solutions for cos(f) are: cf = ( p + q)/(ca2 - 1) cf = (-p + q)/(ca2 - 1)

Dihedral from three angles

Given the three angles: a is angle F-C-Cl b is angle H-C-Cl c is angle H-C-F We want the dihedral angle d (the angle between the two planes defined by F-C-Cl and H-C-Cl).