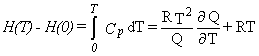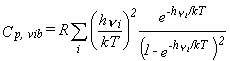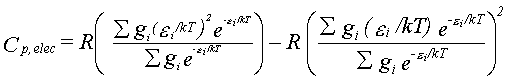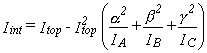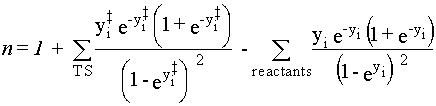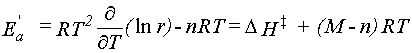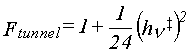Thermochemistry
The following has been adapted from
Computational thermochemistry: prediction amd estimation of molecular thermodynamics
Irikura, K.K.; Frurip, D. J., Eds.;
American Chemical Society, 1998.
Appendix B
Essential Statistical Thermodynamics
Karl K. Irikura
Physical and Chemical Properties Division,
National Institute of Standards and Technology, Gaithersburg, MD 20899
Some computational methods, particularly ab initio techniques,
produce detailed molecular information but no thermodynamic information directly.
Further calculations are needed to generate familiar,
ideal-gas quantities such as the standard molar entropy (S°),
heat capacity (C°p),
and enthalpy change [H° (T)-H° (0)].
This Appendix details the necessary procedures, including worked examples.
Thermochemical calculations can be extended to transition states of chemical reactions.
Procedures are provided for converting such information into rate constants.
Tables are also provided for unit conversions and physical constants.
Statistical thermodynamics calculations are necessary to compute properties as functions of temperature.
In some computations, such as ab initio electronic calculations of molecular energy,
the raw results do not even correspond to properties at absolute zero temperature
and must always be corrected.
All the corrections are based upon molecular spectroscopy,
with temperature-dependence implicit in the molecular partition function, Q.
The partition function is used not only for theoretical predictions,
but also to generate most published thermochemical tables.
Many data compilations include descriptions of calculational procedures (1-3).
Corrections Unique to Ab Initio Predictions
By convention, energies from ab initio calculations are reported in hartrees,
the atomic unit of energy (1 hartree = 2625.5 kJ/mol = 627.51 kcal/mol = 219474.6 cm-1)
(4).
These energies are negative, with the defined zero of energy being the fully-dissociated limit
(free electrons and bare nuclei).
Ab initio models also invoke the approximation that the atomic nuclei are stationary,
with the electrons swarming about them.
This is a good approximation because nuclei are much heavier than electrons.
Consequently, the resulting energies are for a hypothetical, non-vibrating molecule.
Although oscillators may be at rest in classical mechanics,
real (quantum-mechanical) oscillators are always in motion.
The small residual motion at absolute zero temperature is the zero-point vibrational energy,
abbreviated ZPVE or ZPE.
For a simple harmonic oscillator, the ZPE equals one-half the vibrational frequency.
Although all real molecular vibrations are at least slightly anharmonic,
they are usually approximated as harmonic.
Thus, the molecule's ZPE may be taken as one-half the sum of the vibrational frequencies.
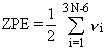 |
Eq. 1 |
In equation 1, N is the number of atoms in the molecule
and the vi are the fundamental vibrational frequencies.
There are 3N-6 vibrations in a non-linear molecule and 3N-5 in a linear molecule;
equation 1 is for the more common non-linear case.
The ZPE must be added to the raw ab initio energy to obtain
an energy corresponding to absolute zero temperature, T = 0 K.
In practice, the ZPE correction is slightly complicated
by the observation that ab initio vibrational frequencies are often in error by +5% to +10%.
To compensate for this error, the computed frequencies are usually multiplied by empirical scaling factors.
The most recent recommendations are those of Scott and Radom (5).
For example, they suggest scaling HF/6-31G* frequencies
by 0.8953 to predict vibrational spectra (i.e., fundamental frequencies),
by 0.9135 for the computation of ZPEs,
by 0.8905 to predict enthalpy differences H° (298.15) - H° (0),
and by 0.8978 to predict S°(298.15).
The methods for computing these quantities are described below.
Common abbreviations and acronyms of the ab initio literature are defined
in the glossary (Appendix D) of this book.
In this Appendix, the degree sign (°) that indicates ideality and standard pressure (1 bar)
is omitted except where the thermal electron convention for ions is being emphasized (see below).
Enthalpies of formation depend upon the thermodynamic conventions for reference states of the elements.
Since this information is not intrinsic to an isolated molecule,
an ab initio reaction energy (i.e., energies for at least two molecules)
must be combined with experimental data to compute an enthalpy of formation,
ΔfH°.
Example: ΔfH°0
of hydrogen fluoride.
There are many levels of approximation in ab initio theory;
several are described in the chapters of this book.
For the present example, we choose the CCSD(T)/aug-cc-pVTZ//B3LYP/6-31G(d) level.
The notation indicates that (1) molecular geometries are calculated
at the density-functional B3LYP level using the 6-31G(d) basis set
and (2) molecular electronic energies are calculated
at the high CCSD(T) level of theory using the rather large aug-cc-pVTZ basis set.
To compute an enthalpy of formation for HF,
we must also choose a balanced chemical reaction for which to calculate an energy.
We choose arbitrarily the reaction shown in equation 2.
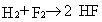 |
Eq. 2 |
Note that the ideal-gas energy and enthalpy are equal at 0 K,
since H = E + PV = E + nRT = E.
The optimized B3LYP/6-31G(d) bond lengths are 0.743, 1.404, and 0.934 Å
for H2, F2, and HF respectively,
in reasonably good agreement with the experimentally derived values
re = 0.741, 1.412, and 0.917 Å respectively (6).
The calculated (harmonic) B3LYP/6-31G(d) vibrational frequencies
are 4451, 1064, and 3978 cm-1
for H2, F2, and HF respectively,
in modest agreement with the experimentally derived harmonic frequencies
ωe = 4401, 917, and 4138 cm-1
respectively (6).
Since 1 cm-1 equals only 0.01196 kJ/mol,
small errors in ZPE will not cause significant errors in the final enthalpy of formation.
Scaling the calculated frequencies by 0.9806 (5)
and substituting them into equation 1 yields
ZPE = 2182, 522, and 1950 cm-1 = 0.009943, 0.002377, and 0.008887 hartree
for H2, F2, and HF respectively.
At these optimized geometries,
the CCSD(T)/aug-cc-pVTZ energies are Ee = -1.172636, -199.313519, and -100.349402 hartree
for H2, F2, and HF respectively.
Adding the ZPEs thus leads to enthalpies (or energies) at T = 0 K of
E0 = -1.162693, -199.311142, and -100.340515 hartree
for H2, F2, and HF respectively.
The calculated enthalpy change is then
ΔrH°0(reaction 2) = -0.207194 hartree = -544.0 kJ/mol.
Using the experimental (defined, in these cases) enthalpies of formation
for H2 and F2 of 0 and 0 kJ/mol (1),
we obtain ΔfH°0(HF) = -272.0 kJ/mol.
This is in good agreement with the experimental value of -272.5 ± 0.8 kJ/mol (1).
All the ab initio calculations for this example were done on a personal computer.
General Relationships of Statistical Thermodynamics
In the present context,
statistical thermodynamics is meant to include the methods
used to convert molecular energy levels into macroscopic properties,
especially enthalpies, entropies, and heat capacities.
Molecular energy levels arise from molecular translation
(i.e., motion through space), rotation, vibration, and electronic excitation.
This information constitutes the spectroscopy of the molecule of interest
and can be obtained experimentally or from calculations.
Partition Function.
The molecular energy levels εi
are used to compute the molecular partition function,
usually denoted by the symbol Q, as shown in equation 3.
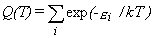 |
Eq. 3 |
The sum extends over all energy levels.
(Sometimes this sum is written only over all unique energy levels,
in which case a level degeneracy gi
must be included in the sum.)
However, for very high temperatures at which the molecule becomes unstable,
the extent of the sum may be ambiguous.
Tabulated thermochemical data must be used with caution under such conditions;
the values (1) may depend strongly upon the high-energy cutoff procedure adopted
and (2) may deviate implicitly from the ideal-gas model.
One typically chooses the lowest energy level to be the zero of energy,
so that no levels lie at negative energies.
From equation 3 it follows that the largest contributions to
Q are from the lowest energy levels.
Conversely, levels that lie far above kT (207 cm-1
at room temperature) have only a minor effect on
Q and its derivative thermodynamic quantities.
Thermodynamic Functions.
Given the partition function,
the usual molar thermodynamic functions can be calculated based upon the following general equations.
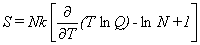 |
Eq. 4 |
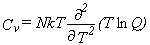 |
Eq. 5 |
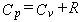 |
Eq. 6 |
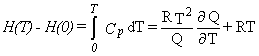 |
Eq. 7 |
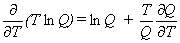 |
Eq. 8 |
 |
Eq. 9 |
 |
Eq. 10 |
 |
Eq. 11 |
Equation 4 is for the entropy, equation 5 for the heat capacity at constant volume,
equation 6 for the heat capacity at constant pressure,
and equation 7 for the enthalpy difference relative to absolute zero temperature.
N is Avogadro's number (6.022137 × 1023),
k is the Boltzmann constant (1.38066 × 1023 J/K),
and the ideal-gas constant R ≡ Nk (4).
The last two terms inside the brackets in equation 4 arise from the indistinguishability
of identical molecules,
which requires a factor of (1/N!) in the partition function for the ensemble.
Expressions 4-7 may more easily be evaluated using equations 8-11 for the various derivatives.
Practical Calculations
A complete set of molecular energy levels is almost never available.
To simplify the problem, one usually adopts a model in which translation,
rotation, vibration, and electronic excitation are uncoupled.
In other words, one makes the approximation that the different types of motion
are unaffected by each other and do not mix together.
This leads to a separability of Q into four factors
that correspond to separate partition functions
for translation, rotation, vibration, and electronic excitation.
This is shown in equation 12,
where the explicit dependence upon temperature has been dropped for simplicity.
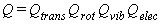 |
Eq. 12 |
When electronically excited states are considered,
one often assumes that the translational, rotational,
and vibrational spectra of the excited state are the same as those of the ground electronic state.
This is crude, but is convenient when no other information is available.
Moreover, if the excited state lies far above kT,
the final results will not be sensitive to such details.
Different energy units are used conventionally in the fields of molecular spectroscopy,
quantum chemistry, and thermochemistry.
To provide some feeling for magnitudes, the values of the thermal energy kT,
at "room temperature" (298.15 K) and at 1000 K,
are listed in Table I in several units.
In this Appendix, all units are of the SI (Système International: kg, m, s, Pa, K)
unless otherwise indicated.
Table I. Thermal energy (kT) at two temperatures, expressed in various units
| Unit |
Room temperature |
1000 K |
| kelvin (K) |
298.15 |
1000 |
| wavenumber (cm-1) |
207.2 |
695.0 |
| Hertz (s-1) |
6.212 × 1012 |
2.084 × 1013 |
| kJ/mol |
2.479 |
8.314 |
| kcal/mol |
0.592 |
1.987 |
| electron volt (eV) |
0.0257 |
0.0862 |
| hartree (atomic unit) |
0.000944 |
0.003167 |
Translational Partition Function.
Rigorously, Qtrans must be calculated from a sum over
all the translational energy levels that are available to a
molecule confined to a cubic box of volume V = RT/p
(molar volume of an ideal gas at temperature T and pressure p).
This is seldom done.
Instead, the sum is approximated as an integral to obtain equations 13-16.
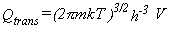 |
Eq. 13 |
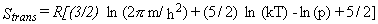 |
Eq. 14 |
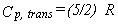 |
Eq. 15 |
![[H(T)-H(0)]trans=(5/2)RT](images/image16.gif) |
Eq. 16 |
This approximation is good as long as
m3/2T5/2p-1 >> h3
(2π)-3/2k-5/2 (3).
At the standard pressure p = 1 bar = 105 Pa = 0.986923 atm,
this condition is met for sufficiently heavy molecules,
m (in amu) >> 11.4 T -5/3,
and for sufficiently high temperatures,
T >> 4.31 m-3/5 (m expressed in amu).
Fortunately, this covers the conditions of common chemical interest.
For an atomic ideal gas, there is no vibrational or rotational motion.
As an example, we can calculate the standard entropy for neon ideal gas at T = 298.15 K.
The atomic mass is converted to SI units using the equivalence
NA amu = 0.001 kg,
where NA = 6.022 × 1023 mol-1
is the Avogadro constant.
Thus for 20Ne (m = 19.992 amu),
m = 3.320 × 10-26 kg.
The values of the physical constants are
h = 6.626 × 10-34 J s,
k = 1.381 × 10-23 J K-1,
and R = kNA = 8.3145 J mol-1 K-1
(7,4).
The standard pressure is p = 105 Pa.
Substituting these values into equation 14 yields
S298.15(20Ne) = 146.21 J mol-1 K-1.
For 21Ne (m = 20.994 amu),
S298.15(21Ne) = 146.82 J mol-1 K-1,
and for 22Ne (m = 21.991 amu),
S298.15(22Ne) = 147.40 J mol-1 K-1.
Averaging these values using the natural abundances of 90.48%, 0.27%, and 9.25%,
respectively (7,8),
we find S298.15 = 146.32 J mol-1 K-1
for the naturally occurring isotopic distribution.
This agrees well with the accepted value of 146.33 J mol-1 K-1
(9).
Rotational Partition Function.
The free rotation of a rigid molecule is also quantized
(the angular momentum and its projection are integer multiples of
h/2π),
so the rotational energy is restricted to certain discrete levels.
Rotational spectra are characterized by the constants
A, B, and C,
where A ≡ h/(8π2IA)
and likewise for B and C.
The quantities IA,B,C are the principal moments of inertia of the molecule,
with the convention IA ≤ IB ≤ IC
(or A ≥ B ≥ C).
Many computer programs, including ab initio packages,
report the rotational constants when provided with a molecular geometry.
The moments can also be calculated manually as the eigenvalues of the inertial tensor,
which has elements like
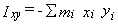 and
and
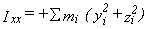 ,
where the index i runs over all atoms in the molecule
and the coordinate origin is at the center of mass.
The product of moments of inertia is all that is needed for the partition function,
not the individual eigenvalues of the inertial tensor,
and the product can be obtained directly from the elements:
,
where the index i runs over all atoms in the molecule
and the coordinate origin is at the center of mass.
The product of moments of inertia is all that is needed for the partition function,
not the individual eigenvalues of the inertial tensor,
and the product can be obtained directly from the elements:
IA IB IC =
Ixx Iyy Izz + 2 Ixy Ixz Iyz
- Ixx Iyz2 - Iyy Ixz2 - Izz Ixy2
Linear molecules (IA = 0) are described by a single rotational constant, B,
and a single moment of inertia, I.
Details may be found in textbooks of molecular spectroscopy.
Fortunately, at high enough temperatures
(kT >> hA),
the sum can be replaced by an integral as it is for translation.
In the general case, the rotational partition function is given by equation 17.
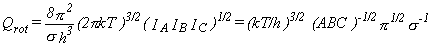 |
Eq. 17 |
For linear molecules, equation 18 should be used instead.
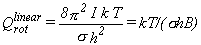 |
Eq. 18 |
In these and subsequent equations, the symbol σ
denotes the "rotational symmetry number" or "external symmetry number" for the molecule.
This is the number of unique orientations of the rigid molecule that only interchange identical atoms.
It preserves parity restrictions on the interchange of identical nuclei when summation
is replaced by integration.
Identifying the correct symmetry number is a common point of difficulty;
it is discussed further below.
For the typical case (equation 17),
the thermodynamic functions are given by equations 19-21.
For linear molecules (equation 18), equations 22-24 are used instead.
External Symmetry Number.
Some computer programs, such as many ab initio packages,
determine the molecular symmetry and external symmetry number (σ) automatically.
If such a program is unavailable, σ may be determined by hand.
With practice, this becomes very fast.
If you are familiar enough with group theory to identify the molecule's point group
(10), then σ can be determined from Table II
(11).
Without identifying the point group,
one can count manually the number of orientations of the rigid molecule
that interchange only identical atoms.
Table II. Symmetry numbers corresponding to symmetry point groups
| Group |
σ |
Group |
σ |
Group |
σ |
Group |
σ |
|---|
| C1, Ci, Cs, C∞v |
1 |
D∞h |
2 |
T, Td |
12 |
Oh |
24 |
| Cn, Cnv, Cnh |
n |
Dn, Dnh, Dnd |
2n |
Sn |
n/2 |
Ih |
60 |
For example, the benzene molecule (C6H6)
belongs to the D6h point group.
From Table II, σ = 12.
Alternatively, one can draw the molecule as a hexagon with numbered vertices.
Rotating the drawing by n × 60°,
where n runs from 0 to 5, generates six different orientations
that are distinguished only by the artificial numbering of the vertices.
Each of these six orientations can be flipped over to generate another orientation,
for a total of 12 unique orientations, σ = 12.
Another example is methyl chloride, CH3Cl.
This belongs to the C3v point group,
so σ = 3.
Alternatively, one can artificially number the hydrogen atoms
and see that there are three unique orientations,
related by rotations of n × 120°
(n = 0-2) around the C-Cl bond axis.
Chlorobenzene, C6H5Cl,
belongs to the C2v point group,
so σ = 2.
Alternatively, one can again number the hydrogen atoms
and see that there are two unique orientations,
related by rotations of n × 180°
(n = 0-1) around the C-Cl bond axis.
In contrast, toluene (C6H5CH3)
belongs to the Cs point group, so σ = 1.
There are no ways to rotate or flip the molecule rigidly that will leave it unchanged.
Allowing the methyl group to rotate leads to an internal
symmetry number which is discussed below,
following the section on internal rotation.
Vibrational Partition Function.
To complete the simple rigid-rotator/harmonic oscillator (RRHO) model,
one must consider the molecular vibrations.
As indicated in the discussion of ZPE (equation 1),
a molecule that contains N atoms
has 3N-6 vibrational frequencies (3N-5 for linear molecules).
The partition function is given in equation 25,
where the product runs over all vibrational frequencies vi.
The corresponding thermodynamic functions are given by equations 26-28.
 |
Eq. 25 |
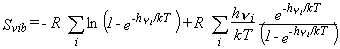 | Eq. 26 |
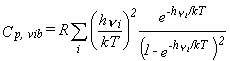 | Eq. 27 |
![[H(T)-H(0)]vib=](images/image30.gif) | Eq. 28 |
Example: Hydrogen Fluoride.
Earlier we used the results of ab initio calculations
to obtain a value for ΔfH°0(HF).
The other equations above permit us to compute ab initio thermodynamic functions,
which will provide an enthalpy of formation at the more useful temperature of 298.15 K.
Results are summarized in Table III.
For simplicity, we will neglect the naturally occurring heavy isotopes of hydrogen.
The molecular weight of 1H19F is 20.006 amu.
Using equation 14, as done above for neon,
leads to Strans = 146.22 J mol-1 K-1.
HF is a linear molecule, so we use equation 22 to calculate Srot.
The ab initio calculation reports a rotational constant
B = 605.64 GHz = 6.0564 × 1011 s-1
based upon the calculated B3LYP/6-31G(d) equilibrium geometry and the most common isotopes.
This molecule belongs to the C∞v point group
(σ = 1);
there are no identical nuclei that can be interchanged by any rotation.
Hence Srot = 27.67 J mol-1 K-1.
For the vibrational contribution,
we scale the B3LYP/6-31G(d) frequency of 3987 cm-1 by 1.0015
as suggested for entropies (5) to obtain ν = 3993 cm-1.
This is multiplied by the speed of light,
c = 2.998 × 1010 cm s-1
(7,4),
to convert wavenumbers to SI frequency units,
ν = 1.197 × 1014 s-1.
Thus hν/kT = 19.27 and equation 26 yields
Svib = 7.22 × 10-7 J mol-1 K-1.
The total entropy is
S298.15 =
Strans +
Srot +
Svib = 173.89 J mol-1 K-1,
in good agreement with the accepted value of 173.78 J mol-1 K-1 (9).
For enthalpy and heat capacity,
the B3LYP/6-31G(d) frequency is scaled by 0.9989 (5) to obtain ν = 3983 cm-1.
The heat capacity Cp(HF) is calculated using equations 15, 23, and 27,
leading to
Cp =
Cp, trans +
Cp, rot +
Cp, vib =
(5/2)R +
R +
1.38 × 10-5 J mol-1 K-1 =
29.10 J mol-1 K-1.
This compares well with the accepted value of 29.14 J mol-1 K-1 (1).
Finally, the enthalpy difference can be computed using equations 16, 24, and 28 to be
[H(298.15)-H(0)] =
(5/2) RT +
RT +
2.14 × 10-4 J mol-1 =
8.68 kJ mol-1.
This can be used to compute ΔfH°298.15(HF) =
ΔfH°0(HF) +
[H(298.15)-
H(0)]HF -
[H(298.15)-H(0)]elements.
Taking the ab initio value ΔfH°0(HF) =
-272.0 kJ/mol from above,
the calculated enthalpy difference of 8.68 kJ/mol for HF,
and the accepted enthalpy differences of (8.47)/2 and (8.83)/2 kJ/mol
for (1/2)H2 and (1/2)F2 (9),
we obtain ΔfH°298.15(HF) = -272.0 kJ/mol,
in agreement with the accepted value of -273.3 ± 0.7 kJ mol-1 (9)
[-272.5 ± 0.8 kJ/mol is listed in older ref (1)].
Table III. Results for Hydrogen Fluoride Example
| Contribution |
S, J/(mol K) |
Cp, J/(mol K) |
[H(298.15)-H(0)], kJ/mol |
|---|
| Translation |
146.22 |
20.79 |
6.20 |
| Rotation |
27.67 |
8.31 |
2.48 |
| Vibration |
7 × 10-7 |
1 × 10-5 |
2 × 10-4 |
| Total |
173.89 |
29.10 |
8.68 |
Electronic Partition Function.
Although they may not have low-lying electronic excited states,
some molecules have degenerate electronic ground states.
Free radicals are a common example.
They may have unpaired electrons in their electronic ground states
and a net electron spin of S = nunpaired/2,
where nunpaired is the number of unpaired electrons.
(Beware not to confuse the spin quantum number S with the entropy.)
The multiplicity, or degeneracy g, of such a state is g = (2S+1).
Using degeneracy numbers is equivalent to an explicit count of all states, including degenerate ones.
Thus, Qelec = g is a constant and only affects the entropy:
Selec = Rln(g) and
Cp, elec = [H(T)-H(0)]elec = 0.
Since most free radicals have only a single unpaired electron,
the usual effect is to increase the entropy by Rln(2).
In addition to spin degeneracies, some states have spatial degeneracies.
This situation is most common for diatomic molecules.
Linear molecules with a spatial symmetry other than Σ
(e.g., Π or Δ)
have a spatial degeneracy of 2.
For example, the OH radical has a 2Π ground state,
so its degeneracy is g = 2 (spin) × 2 (spatial) = 4.
If there are both spin and spatial degeneracies, spin-orbit coupling lifts the degeneracy, often significantly.
In the example of OH, the 4-fold degenerate ground state is split into
two doubly-degenerate levels separated by 139.2 cm-1 (6).
In such a case the low-lying excited states should be included in the calculation of thermodynamic quantities.
The partition function is given by equation 29,
where εi
and gi are the excitation energies (spectroscopic T0)
and degeneracies of the excited states,
g0 and ε0 ≡ 0
are for the ground state, and the sum runs over all the electronic states being considered,
including the ground state.
The contributions to the thermal functions are given by equations 30-32.
This treatment assumes, rather crudely,
that the rotations and vibrations are unaffected by electronic excitation.
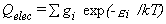 | Eq. 29 |
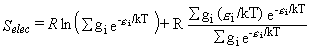 | Eq. 30 |
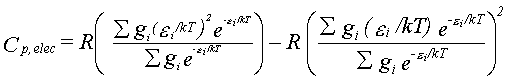 | Eq. 31 |
![[H(T)-H(0)]elec=](images/image34.gif) | Eq. 32 |
Example: Entropy of Methyl Radical.
For simplicity, we again neglect minor isotopes.
Results are summarized in Table IV.
The molecular weight of CH3 is then m = 15.023 amu,
so Strans = 142.65 J mol-1 K-1.
This is a flat, triangular molecule that belongs to the D3h point group,
σ = 6.
The experimental bond length is re = 1.0767 Å =
1.0767 × 10-10 m (12-14).
The moments of inertia can be evaluated using the symmetry of this oblate top,
or more generally by diagonalizing the inertial tensor.
We place the molecule in the yz plane with one hydrogen atom on the z axis.
The center of mass coincides with the carbon atom.
The cartesian coordinates then lead to an inertial tensor with components
Ixx = 3mHre2,
Ixy = Iyx = 0,
Ixz = Izx = 0,
Iyy = (3/2)mHre2,
Iyz = Izy = 0, and
Izz = (3/2)mHre2 = 2.910
× 10-47 kg m2.
This is already diagonal, with eigenvalues
IA =
IB = 2.910 × 10-47 kg m2 and
IC = 5.820 kg m2
so that Srot = 43.50 J mol-1 K-1 (equation 19).
The observed vibrational frequencies of CH3 are
3004.4, 606.5, 3160.8, and 1396 cm-1
for ν1, ν2,
ν3, and ν4 respectively (15).
Since ν3 and ν4
are both doubly degenerate (e′ symmetry),
they are counted twice and we have the correct number of vibrations, 3N-6 = 6.
Converting to SI units leads to Svib =
6.51 × 10-5 + 1.84 +
6.42 × 10-5 + 0.15 =
1.99 J mol-1 K-1.
In this case, this is a radical with one unpaired electron, S = 1/2
(electronic ground state is 2A2″),
so the degeneracy g = 2 and Selec = Rln(2).
Adding the four contributions to the entropy gives S298.15 =
193.9 J mol-1 K-1,
in agreement with the literature value of 194.2 ± 1.3 J mol-1 K-1 (1).
Example: Entropy of Hydroxyl Radical.
For simplicity, we again neglect minor isotopes.
Results are summarized in Table IV.
The molecular weight of OH is then m = 17.003 amu,
so Strans = 144.19 J mol-1 K-1.
Again using the simple RRHO model,
the observed bond length is re = 0.96966 Å (6)
and the symmetry number σ = 1
(C∞v point group).
Hence I = 1.480 × 10-47 kg m2
and Srot = 28.22 J mol-1 K-1.
Using the observed vibrational fundamental for the vibrational frequency,
ν = ω0 = 3568 cm-1 (6) leads to
Svib = 5.04 × 10-6 J mol-1 K-1.
If spin-orbit splitting is ignored, Qelec = 4 as explained above,
so Selec = 11.53 J mol-1 K-1.
Combining these four contributions yields S = 183.9 J mol-1 K-1.
If instead the spin-orbit splitting is included,
so that g0 = g1 = 2 and
ε1 = 139.2 cm-1 =
2.765 × 10-21 J,
then equation 30 yields Selec = 11.08 J mol-1 K-1
and so the total S = 183.5 J mol-1 K-1.
The literature value is 183.71 ± 0.04 J mol-1 K-1 (1).
Table IV. Methyl and Hydroxyl Examples,
S°298, J/(mol K)
| Contribution |
Methyl |
Hydroxyla |
Hydroxylb |
|---|
| Translation |
142.65 |
144.19 |
144.19 |
Rotation |
43.50 |
28.22 |
28.22 |
| Vibration |
1.99 |
5 × 10-6 |
5 × 10-6 |
| Electronic |
5.76 |
11.53 |
11.08 |
| Total |
193.9 |
183.9 |
183.5 |
aSpin-orbit splitting ignored.
bSpin-orbit splitting included.
Internal Rotation.
This refers to torsional motion, most commonly involving methyl groups.
There are three ways to treat such a rotor, depending upon its barrier to rotation.
The free and hindered rotor models require that an internal symmetry number,
σint, be included.
σint equals the number of minima (or maxima)
in the torsional potential energy curve.
The harmonic oscillator model does not require σint
because it ignores all but one of the energy minima.
For intermediate barrier heights (hindered rotor),
the appropriateness of an internal symmetry number may be confusing.
In such cases, avoid over- or under-counting states by ensuring that the
limiting case of infinite barriers
(harmonic oscillator model, no σint)
moves smoothly into the limiting case of zero barrier
(free rotor model, σint needed) as the barrier height decreases.
Note that the vibrational frequency corresponding to the torsion must be deleted
if the torsion is treated as a free or hindered rotation.
Free Rotor.
If the barrier to rotation is much less than kT,
then the rotor may be considered freely rotating.
For a symmetric rotor such as a methyl group, the partition function is given by equation 33,
where Iint is the reduced moment of inertia for the internal rotation
and is given by equation 34 (3).
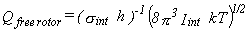 | Eq. 33 |
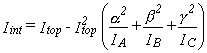 | Eq. 34 |
Asymmetric rotors can be treated using an appropriate formula for the reduced moment (3).
In equation 34, Itop is the moment of inertia of the rotating fragment
about the axis of internal rotation.
This is expressed as 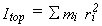 ,
where the mi are atomic masses,
ri is the distance of atom i from the axis of internal rotation,
and the sum runs over all atoms in the rotating fragment.
The quantities
α, β, γ
are the cosines of the angles formed between the internal rotation axis
and the principal axes of the overall molecule that correspond to
IA, IB, and IC, respectively.
Contributions to the thermodynamic functions are given in equations 35-37.
,
where the mi are atomic masses,
ri is the distance of atom i from the axis of internal rotation,
and the sum runs over all atoms in the rotating fragment.
The quantities
α, β, γ
are the cosines of the angles formed between the internal rotation axis
and the principal axes of the overall molecule that correspond to
IA, IB, and IC, respectively.
Contributions to the thermodynamic functions are given in equations 35-37.
Harmonic Oscillator.
If the barrier to internal rotation is much greater than kT,
one can consider the torsion to be a non-rotating, harmonic oscillator.
Treatment is the same as for other vibrations.
Hindered Rotor.
This is the common, intermediate case, when the torsional barrier V is comparable to kT.
If the torsional potential is assumed to have the simple form
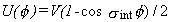 ,
then the tables of Pitzer and Gwinn are usually used to compute the contribution of the hindered rotor
to the thermodynamic functions (16,17).
Their tables are in terms of the dimensionless variables x and y,
where
,
then the tables of Pitzer and Gwinn are usually used to compute the contribution of the hindered rotor
to the thermodynamic functions (16,17).
Their tables are in terms of the dimensionless variables x and y,
where 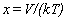 and
and
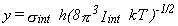 and Iint is defined as for a free rotor (see above).
and Iint is defined as for a free rotor (see above).
Example: Entropy of Ethane at T = 184 K [adapted from ref (17)].
Results are summarized in Table V.
Ignoring minor isotopes as before, for C2H6 we have m = 30.047 amu,
so Strans = 141.26 J mol-1 K-1.
The experimental geometry is staggered (D3d point group, σ = 6)
and defined by rCC = 1.535 Å,
rCH = 1.094 Å, and
θCCH = 111.2° (12-14).
If we choose coordinates so that the origin is at the center of mass,
the carbon atoms lie on the z-axis,
and the yz plane is a reflection plane of symmetry, then the elements of the inertial tensor are,
in (amu Å2),
Ixx = Iyy = 25.46,
Ixy = Iyx =
Ixz = Izx =
Iyz = Izy = 0, and
Izz = 6.291 amu Å2.
This is already diagonal,
with eigenvalues
IA = 1.045 × 10-46 kg m2
and
IB =IC = 4.228 × 10-46 kg m2
so that Srot = 62.17 J mol-1 K-1 (equation 19).
The observed vibrational frequencies (18) are
2954, 1388, 995, 289 (torsion), 2896, and 1379 cm-1 (non-degenerate),
and 2969, 1468, 1190, 2985, 1469, and 822 cm-1 (doubly degenerate),
for a total of 3N-6 = 18 vibrational modes and
Svib = 3.36 J mol-1 K-1
(0.25 J mol-1 K-1 excluding the torsional mode).
The total entropy in the RRHO model is thus
S°184 = 206.8 J mol-1 K-1,
which is below the experimental value S = 207.7 ± 0.6 J mol-1 K-1 (17).
If we consider the torsion to be a free, unhindered rotor,
then we require the corresponding reduced moment of inertia.
In this case, in the rotor axis is aligned with the A axis of the molecule,
so that α = 1
and β = γ= 0 in equation 34.
This gives Iint =
Itop - Itop2/IA.
The symmetry of this molecule requires that IA = 2Itop,
because the moment of inertia of the whole molecule around the A axis
(viz., the C-C bond axis) is twice that of a single methyl group.
Thus Iint = 2.613 × 10-47 kg m2.
The internal symmetry number is σint = 3,
since there are three equivalent values of the torsion angle (0°, 120°, and 240°).
Equation 35 yields Sfree rotor = 10.09 J mol-1 K-1,
for a total entropy of S°184 = 213.8 J mol-1 K-1
in the free-rotor model, which is higher than the experimental value.
To apply the hindered-rotor model we need a value for the torsional barrier height.
This can be estimated from the observed torsional vibrational frequency ν
(in s-1) as V
≈ 8π2Iintν2/
σint2 =
1.720 × 10-20 J (or 10.4 kJ/mol).
Thus the parameters are x = 6.77 and y = 0.490.
Interpolating within the standard tables
(16,17),
Shindered rotor = 3.99 J mol-1 K-1,
so that the total entropy is S = 207.7 J mol-1 K-1,
in agreement with the experimental value.
Table V. Ethane Example, S°184 (J mol-1 K-1)
| Contribution |
Harmonic Rotor |
Free Rotor |
Hindered Rotor |
|---|
| Translation |
141.26 |
141.26 |
141.26 |
| Rotation |
62.17 |
62.17 |
62.17 |
| Vibration |
0.25 |
0.25 |
0.25 |
| Torsion |
3.11 |
10.09 |
3.99 |
| Total |
206.8 |
213.8 |
207.7 |
Charged Molecules: Two Conventions.
The balanced chemical equation describing an ionization process involves at least one free electron.
There are two major conventions for the thermodynamic properties of the electron.
Most compilations of thermochemical data adopt the thermal electron convention.
In this convention, the free electron is treated as a chemical element,
so that its ideal-gas enthalpy of formation is zero at all temperatures.
In contrast, most of the literature in mass spectrometry and ion chemistry adopts the ion convention,
sometimes also called the stationary electron convention.
In this convention, the enthalpy content of the electron is ignored.
At absolute zero temperature there is no difference between the two conventions,
but in general enthalpies of formation under the two conventions are related by equation 38,
where q is the (signed) charge on the ion in question (±1 in most cases).
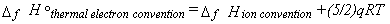 |
Eq. 38 |
A thorough discussion is provided in the introduction to the GIANT tables (19).
When reporting the thermochemistry of ions,
it is important always to indicate which convention is being used.
Especially beware not to combine enthalpies of formation that were derived using different conventions.
Chemical Kinetics
The equilibrium constant for a reaction is
Keq = exp(-ΔG/RT),
where
ΔG =
ΔH -
TΔS
and the differences are between the reactants and products, e.g.,
ΔS =
Sproducts -
Sreactants.
Simple transition-state theory for chemical kinetics assumes that
the reaction rate is limited by formation of a transient transition state,
which is the point of maximum energy along the path from reactants to products.
The transition state is considered to be in quasi-equilibrium with the reactants.
If differences between reactants and the transition state are denoted with a double dagger,
e.g., ΔS‡ = STS - Sreactants,
then the rate constant (denoted r here to avoid confusion with the Boltzmann constant)
is given by equation 39.
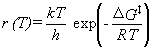 |
Eq. 39 |
As for stable species,
ΔG‡ =
ΔH‡ -
TΔS‡.
Thus rate constants can be calculated easily from the "thermochemistry" for transition states.
In such calculations, the imaginary vibrational frequency is ignored,
so that there are only 3N-7 molecular vibrations in the transition structure (3N-6 if linear).
If all internal and external symmetry numbers are included in the rotational partition functions,
then any reaction path degeneracy will usually be included automatically.
Occasionally, however, stereochemical factors are also needed (20).
Experimental, temperature-dependent rate constants are often presented as
an Arrhenius plot of r(T) vs. 1/T.
This is motivated by the observation that such plots are nearly linear,
r(T) = A exp(-Ea/RT),
where the pre-exponential factor A is usually called simply the A-factor
and Ea is the phenomenological activation energy.
It is often desirable to report A and Ea in computational studies,
for comparison with the values derived from experimental data.
They may be determined using equations 40 and 41,
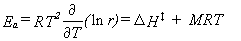 |
Eq. 40 |
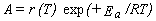 |
Eq. 41 |
where M is the molecularity of the reaction
(e.g., M = 1 for a unimolecular and M = 2 for a bimolecular reaction).
The derived A and Ea are weakly temperature-dependent.
This is consistent with experimental results,
which are often fitted using the three-parameter modified Arrhenius expression
r(T) = A' Tn exp(-E'a/RT).
This functional form leads to a better fit than the ordinary Arrhenius expression,
but the parameters may have little physical interpretation.
If the RRHO approximation is accepted,
then the three parameters are given by equations 42-44,
where the yi in equation 42 are the reduced vibrational frequencies,
yi = hνi/kT.
However, in practice it is often best to determine the parameters A',
n, and E'a
by fitting calculated rate constants to the modified Arrhenius expression.
Ab initio energies are now precise enough that it is becoming common
to use kinetic theories more sophisticated than simple transition-state theory.
When the reaction coordinate is dominated by motion of a hydrogen atom,
corrections for quantum-mechanical tunneling are often made (21).
The simplest is the Wigner correction,
which requires only the imaginary vibrational frequency
ν‡i
associated with the reaction coordinate.
To apply this correction, the calculated rate is multiplied by Ftunnel (equation 45).
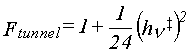 |
Eq. 45 |
Better results may be obtained by
fitting the energy profile of the reaction to an Eckart potential function
(see the chapter by Petersson in this book).
The location of the transition state can also be refined.
Variational transition-state theory defines the transition state as the maximum
in the free energy along the reaction path,
instead of the maximum along the vibrationless potential energy curve.
Such a definition is essential for reactions such as simple bond cleavage,
which usually has no barrier in excess of the bond energy.
Units and Constants
In actual calculations, many practical difficulties involve incompatible units.
In addition to the standard units of the SI, many others are in use,
usually for historical reasons.
Conversion factors among selected units are provided in Table VI.
For convenience, the values of commonly-used constants are collected in Table VII.
Detailed information is available on-line at
http://www.physics.nist.gov/PhysRefData/contents.html.
Table VI. Unit Conversions
| Quantity |
Unit |
Conversiona |
SI Unit |
|---|
| energy |
hartree (atomic unit) |
2625.500 |
kJ/mol |
| energy |
cal |
4.184 |
J |
| energy |
cm-1 (wavenumber) |
0.01196266 |
kJ/mol |
| energy |
eV |
96.48531 |
kJ/mol |
| energy |
K (temperature) |
8.314511 × 10-3 |
kJ/mol |
| distance |
Å |
10-10 |
m |
| distance |
bohr (atomic unit) |
5.291772 × 10-11 |
m |
| mass |
amu or u |
1.660540 × 10-27 |
kg |
| pressure |
bar |
105 |
Pa |
| pressure |
atm |
101325 |
Pa |
| pressure |
Torr or mm-Hg |
133.32237 |
Pa |
| pressure (density) |
cm-3 (at 298.15 K; ideal gas) |
4.16643 × 10-15 |
Pa |
| pressure (density) |
cm-3 (arb. temp.; ideal gas) |
106 kT |
Pa |
| pressure (density) |
M or mol/L (ideal gas) |
103 RT |
Pa |
| dipole moment |
atomic unit |
8.478358 × 10-30 |
C m |
| dipole moment |
D (debye) |
3.335641 × 10-30 |
C m |
aMultiply the quantity expressed in the units of column 2
by the conversion factor in column 3
to obtain the quantity expressed in units of column 4 (SI units).
Table VII. Physical Constants
| Quantity |
Value |
|---|
| k |
1.38066 × 10-23 J K-1 |
| NA |
6.022137 × 1023 mol-1 |
| R = kNA |
8.314510 J mol-1 K-1 |
| h |
6.626076 × 10-34 J s |
| c |
299792458 m s-1 |
Literature Cited
By selecting these links, you will be leaving
NIST webspace. We have provided these
links to other web sites because they may
have information that would be of interest to
you. No inferences should be drawn on
account of other sites being referenced, or
not, from this page. There may be other
web sites that are more appropriate for your
purpose. NIST does not necessarily endorse
the views expressed, or concur with the
facts presented on these sites. Further, NIST
does not endorse any commercial products
that may be mentioned on these sites. Please
address comments about this page to
[email protected]
1. Chase, M. W., Jr.; Davies, C. A.; Downey, J. R., Jr.; Frurip, D. J.; McDonald, R. A.; Syverud, A. N. J. Phys. Chem. Ref. Data 1985, 14, Suppl. 1.
2. Thermodynamic Properties of Individual Substances; 4th ed.; Gurvich, L. V.; Veyts, I. V.; Alcock, C. B., Eds.; Hemisphere: New York, 1989.
3. Frenkel, M.; Marsh, K. N.; Wilhoit, R. C.; Kabo, G. J.; Roganov, G. N. Thermodynamics of Organic Compounds in the Gas State; Thermodynamics Research Center: College Station, Texas, 1994; Vol. I.
4. Cohen, E. R.; Taylor, B. N. The 1986 CODATA Recommended Values of the Fundamental Physical Constants; http://physics.nist.gov/PhysRefData.
5. Scott, A. P.; Radom, L. J. Phys. Chem. 1996, 100, 16502.
6. Huber, K. P.; Herzberg, G. Molecular Spectra and Molecular Structure: IV. Constants of Diatomic Molecules; van Nostrand Reinhold: New York, 1979.
7. CRC Handbook of Chemistry and Physics; 76th ed.; Lide, D. R.; Frederikse, H. P. R., Eds.; CRC Press: Boca Raton, 1995.
8. Winter, M. WebElements; http://www.webelements.com.
9. Cox, J. D.; Wagman, D. D.; Medvedev, V. A. CODATA Key Values for Thermodynamics; Hemisphere: New York, 1989.
10.
Cotton, F. A. Chemical Applications of Group Theory; 2nd ed.; Wiley--Interscience: New York, 1971.
11. Herzberg, G. Molecular Spectra and Molecular Structure: II. Infrared and Raman Spectra of Polyatomic Molecules; van Nostrand: New York, 1945.
12. Structure Data of Free Polyatomic Molecules; Kuchitsu, K., Ed.; Landolt-Börnstein New Series; Madelung, O., Ed.; Springer: Berlin, 1992; Vol. II:21.
13. Structure Data of Free Polyatomic Molecules; Hellwege, K.-H.; Hellwege, A. M., Eds.; Landolt-Börnstein New Series; Madelung, O., Ed.; Springer: Berlin, 1987; Vol. II:15.
14. Structure Data of Free Polyatomic Molecules; Hellwege, K.-H.; Hellwege, A. M., Eds.; Landolt-Börnstein New Series; Hellwege, K.-H., Ed.; Springer: Berlin, 1976; Vol. II:7.
15. Jacox, M. E. Vibrational & Electronic Energy Levels of Small Polyatomic Transient Molecules (VEEL): Version 4.0; NIST-SRD 26 (electronic database); Natl. Inst. of Standards and Technology: Gaithersburg, MD, 1995.
16. Pitzer, K. S.; Gwinn, W. D. J. Chem. Phys. 1942, 10, 428.
17. Janz, G. J. Thermodynamic Properties of Organic Compounds; Academic: New York, 1967.
18. Shimanouchi, T. Tables of Molecular Vibrational Frequencies, Consolidated Volume I; NSRDS-NBS 39; U.S. GPO: Washington, D.C., 1972.
19. Lias, S. G.; Bartmess, J. E.; Liebman, J. F.; Holmes, J. L.; Levin, R. D.; Mallard, W. G. J. Phys. Chem. Ref. Data 1988, 17, Suppl. 1.
20. Gilbert, R. G.; Smith, S. C. Theory of Unimolecular and Recombination Reactions; Blackwell Scientific: Oxford, 1990.
21. Bell, R. P. The Tunnel Effect in Chemistry; Chapman and Hall: London, 1980.