Computational Chemistry Comparison and Benchmark DataBase Release 22 (May 2022) Standard Reference Database 101 National Institute of Standards and Technology
	Home All data for one species Geometry Experimental Experimental Geometries Same bond/angle many molecules Internal Coordinates by type Bond angles Calculated Calculated geometry Rotational constant Moments of inertia Products of moments of inertia BSE Bond lengths Show me a calculated geometry Comparisons Bonds, angles Rotational Constants Products of moments of inertia Point group Bad Calculations Bad moment of inertia Tutorials and Explanations Angle formulas Vibrations Experimental Vibrational frequencies Calculated Frequencies Scale factors Reactions Entropies Ions List Ions Energy Calculated Ionization Energy Compare Ionzation energy Electron Affinity Calculated Electron affinity Compare Electron affinity Proton Affinity Calculated Proton affinity Compare Proton affinity Ionization changes point group Experimental One molecule all properties One property a few molecules Enthalpy of formation Entropy Integrated Heat Capacity Heat Capacity Rotational Constants Vibrational Frequencies Dipole moment Ionization Energy Polarizability Quadrupole Point Groups Geometry Experimental Geometries Internal Coordinates by type Bond angles Rotational Constants Point Groups Diatomic bond lengths Vibrations Vibrational frequencies Diatomic Triatomics Energy Atomization Energy Internal Rotation Electrostatics Dipole Quadrupole Polarizability Reference Data Reference states Spin Splittings Molecules with good enthalpy Enthalpy at 0 Kelvin Calculated Energy Optimized Energy Energy 298K Minimum conformation Hydrogen bonds H bond with counterpoise Reaction Reaction Energy 0K Reaction Energy 298K Internal Rotation Barriers to internal rotation Rotational barrier and dipole Rotational Barrier 2 molecules Orbital HOMO LUMO gap HOMO Orbital Energies Nuclear repulsion energy Correlation Full vs Frozen core energies Partial correlation energies Ion Calculated Ionization Energy Vertical ionization Energy Calculated Electron affinity Calculated Proton affinity Atom charge differences Excited State Singlet triplet gap Electronic state Transition state Basis Set Extrapolation BSE energy BSE Bond lengths Geometry Calculated geometry AIM bond orders One type of bond Rotation Rotational constant Products of moments of inertia Moments of inertia Inertial defects Second moments Point group State symmetry <r2> Sorted by r2 Z-matrix Bad Calculations Bad moment of inertia Bad Calculated Bond Lengths Bad point group Worst molecules Vibrations Frequencies Animated vibrations Anharmonic Zero point energy (ZPE) Scale Factors Scale factors Scale factor uncertainty Calculate a scale factor Why scale vibrations Set scaling factors Bad Calculations Bad Vib. HF vs MP2 Bad vib. Calc. vs exp. Big anharmonicity Electrostatics Charges Mulliken CHELP Aim ESP Dipole Dipole Dipole angle Dipole calculation types Quadrupole Polarizability Spin Spin density Entropy and Heat Capacity Entropy Reaction entropy Heat Capacity Reaction Reaction Energy 0K Reaction Energy 298K Isodesmic reactions Transition State Transition state Transition state frequencies Transition state geometries IRC Lookup by property By frequency Comparisons Geometry Bonds, angles Bond, angle, or dihedral DFT grid size on point group DFT grid on bond length Core correlation - bond length Same bond/angle many molecules Isoelectronic diatomics Isoelectronic triatomic angles Average bond lengths Rotation Rotational Constants Products of moments of inertia Point group Vibrations Vibrations 2 calculations Frequency differences One frequency Zero point energy Intensity Intensity for one mode Vibrational intensities Reduced mass comparison Anharmonic Triatomic Scale factors Energy Reaction Reaction Energy 0K Reaction Energy 298K Atomization 0K Atomization 298K Single point vs optimized DFT grid size on energy Semiempirical enthalpy Internal rotation Similar molecules Conformation Sets of isomers Sets of tautomers Isomers Entropy Entropy Heat capacity Entropy of several molecules Integrated heat capacity Reaction entropy Electrostatics Dipole Polarizability Several molecules Quadrupole Ion Compare Ionzation energy Koopman ionization energy Koopman IE for a few molecules Compare Electron affinity Compare Proton affinity Protonation Site Resources Info on Results Calculations Done Method and basis set List molecules One molecule Multiple conformers, states Multiple conformers, states Basis functions used I/O files Input/output files MOL file Z-matrix wfn files Glossary Conversion Forms B to I, I to B Angle formulas Integrated heat Capacity Calculating Enthalpy Links NIST Links NIST webbook bibliographic data CCCBDB Experimental data External links Basis Set Exchange Computational Chemistry List Thermochemistry in Gaussian Minnesota Database Collection Benchmark Energy and Geometry Point Groups Thermochemistry Thermochemistry Molecules with good enthalpy A → B + C Reference states Tutorials Vibrations Why scale vibrations Zero-point energies Entropy Methyl rotor entropy Entropy and conformations Energy Getting enthalpy of formation Vertical vs adiabatic IE Thermo from calculations Electrostatics Dipole parts by point group Quadrupoles Geometry Angle formulas Cost Cost Comparison Timings Comparison Bad Calculations Geometry Bad moment of inertia Bad Calculated Bond Lengths Bad point group Worst molecules Vibrations Bad vib. Calc. vs exp. Bad Vib. HF vs MP2 Bad scale factors Low excited states Oddities NaCN Is not linear FAQ Help Units Choose Units Energy Bond length Rotational Constant Moment of Inertia Dipole and Quadrupole Polarizability Explanations Hartree cm-1 Debye Credits Just show me Show me a calculated geometry Summary Using older interface Limit Basis sets Method options List Recent molecules Choose a few Molecules Number of atoms By heavy atoms Diatomics InChI Deuterated Dimers Geometry Point group Point group count Bonds types Isodesmic reactions Bad point group Multiple conformers, states Vibrations Big anharmonicity Energy Enthalpy at 0 Kelvin Similar molecules Similar Isomers Cis/trans Tautomers Multiple conformers, states Ions, Dipoles, etc. List Ions Ionization changes point group Dipole Quadrupole Polarizability Proton Affinities Index of CCCBDB Feedback Error form Wants
You are here: Calculated > Vibrations > Scale Factors > Why scale vibrations OR Resources > Tutorials > Vibrations > Why scale vibrations

Vibrational scaling factors

The vibrational frequencies produced by ab initio programs are often multiplied by a scale factor (in the range of 0.8 to 1.0) to better match experimental vibrational frequencies. This scaling compensates for two problems:
1) The electronic structure calculation is approximate. Usually less than a relativistic full configuration interaction is performed.
2) The potential energy surface is not harmonic. For bond stretches a better description of the potential energy surface is given by the Morse potential E(x) = D(1-exp(-β( x-x₀ )))² illustrated below. In this equation E is the potential energy, D, β, and x₀ are constants, and x is the interatomic distance.

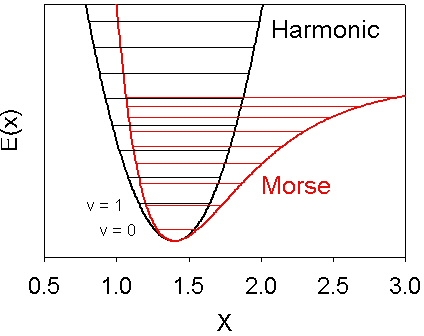
The programs that predict vibrational frequencies do so by calculating the second derivative of the potential energy surface with respect to the atomic coordinates. This provides the curvature at the bottom (minimum) of the well. For a harmonic potential E(x) = k x ² this is directly related to the vibrational energy level spacing. For a Morse potential (with the same second derivative at the minimum) the anharmonicity causes the vibrational energy levels to be more closely spaced as illustrated in the figure.

Experimentally usually the fundamental (v=0 to v=1 energy) is measured. If enough vibrational levels are observed a harmonic frequency can be estimated with a formula such as G(v) = ω_e(v+1/2) - ω_ex_e(v+1/2)² + ω_ey_e(v+1/2)³ + ... where G(v) is the vibrational energy, v is the vibrational quantum number, ω_e is the harmonic frequency, and ω_ex_e and ω_ey_e are anharmonic constants. For polyatomic molecules usually only the fundamental is experimentally observed.

How we calculate the vibrational scaling factors

How much do the factors change with basis set?

The scaling factors depend weakly on basis set. The uncertainties are about twice as large for the 3-21G basis set as for the other basis sets, all of which include polarization functions. This suggests that polarization functions are important for avoiding markedly poor predictions of vibrational frequencies. For larger basis sets the scaling factors and uncertainties have non-significant changes. Thus the same scaling factors can be used for other basis sets.