Jump to
S1C2
S1C3
Energy calculated at CCD/6-31G
| | hartrees |
|---|
| Energy at 0K | -165.874616 |
| Energy at 298.15K | |
| HF Energy | -165.601993 |
| Nuclear repulsion energy | 49.056636 |
The energy at 298.15K was derived from the energy at 0K
and an integrated heat capacity that used the calculated vibrational frequencies.
Vibrational Frequencies calculated at CCD/6-31G
| Mode Number |
Symmetry |
Frequency
(cm-1) |
Scaled Frequency
(cm-1) |
IR Intensities
(km mol-1) |
Raman Act
(Å4/u) |
Dep P |
Dep U |
|---|
| 1 |
A1 |
4064 |
3900 |
9.93 |
|
|
|
| 2 |
A1 |
780 |
749 |
5.37 |
|
|
|
| 3 |
A1 |
393 |
377 |
153.17 |
|
|
|
| 4 |
A1 |
235 |
225 |
434.47 |
|
|
|
| 5 |
A2 |
101i |
97i |
0.00 |
|
|
|
| 6 |
B1 |
381 |
366 |
58.30 |
|
|
|
| 7 |
B2 |
4063 |
3899 |
300.21 |
|
|
|
| 8 |
B2 |
1658 |
1591 |
439.69 |
|
|
|
| 9 |
B2 |
170 |
163 |
95.17 |
|
|
|
Unscaled Zero Point Vibrational Energy (zpe) 5821.3 cm
-1
Scaled (by 0.9595) Zero Point Vibrational Energy (zpe) 5585.6 cm
-1
See section
III.C.1 List or set vibrational scaling factors
to change the scale factors used here.
See section
III.C.2
Calculate a vibrational scaling factor for a given set of molecules
to determine the least squares best scaling factor.
Geometric Data calculated at CCD/6-31G
Point Group is C2v
Cartesians (Å)
| Atom |
x (Å) |
y (Å) |
z (Å) |
|---|
| Be1 |
0.000 |
0.000 |
-0.008 |
| O2 |
0.000 |
1.412 |
0.031 |
| O3 |
0.000 |
-1.412 |
0.031 |
| H4 |
0.000 |
2.327 |
-0.230 |
| H5 |
0.000 |
-2.327 |
-0.230 |
Atom - Atom Distances (Å)
| |
Be1 |
O2 |
O3 |
H4 |
H5 |
| Be1 | | 1.4124 | 1.4124 | 2.3375 | 2.3375 |
O2 | 1.4124 | | 2.8238 | 0.9512 | 3.7478 | O3 | 1.4124 | 2.8238 | | 3.7478 | 0.9512 | H4 | 2.3375 | 0.9512 | 3.7478 | | 4.6538 | H5 | 2.3375 | 3.7478 | 0.9512 | 4.6538 | |
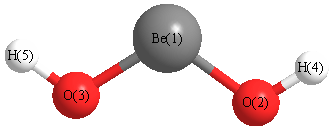 More geometry information
More geometry information
Calculated Bond Angles
| atom1 |
atom2 |
atom3 |
angle |
|
atom1 |
atom2 |
atom3 |
angle |
| Be1 |
O2 |
H4 |
162.585 |
|
Be1 |
O3 |
H5 |
162.585 |
| O2 |
Be1 |
O3 |
176.905 |
|
Electronic energy levels
Charges, Dipole, Quadrupole and Polarizability
Jump to
S1C1
S1C3
Energy calculated at CCD/6-31G
| | hartrees |
|---|
| Energy at 0K | -165.874647 |
| Energy at 298.15K | -165.875450 |
| HF Energy | -165.601840 |
| Nuclear repulsion energy | 49.019194 |
The energy at 298.15K was derived from the energy at 0K
and an integrated heat capacity that used the calculated vibrational frequencies.
Vibrational Frequencies calculated at CCD/6-31G
| Mode Number |
Symmetry |
Frequency
(cm-1) |
Scaled Frequency
(cm-1) |
IR Intensities
(km mol-1) |
Raman Act
(Å4/u) |
Dep P |
Dep U |
|---|
| 1 |
A |
4058 |
3893 |
5.37 |
|
|
|
| 2 |
A |
778 |
747 |
2.76 |
|
|
|
| 3 |
A |
385 |
370 |
107.81 |
|
|
|
| 4 |
A |
231 |
221 |
216.22 |
|
|
|
| 5 |
A |
110 |
106 |
289.90 |
|
|
|
| 6 |
B |
4057 |
3893 |
295.98 |
|
|
|
| 7 |
B |
1655 |
1588 |
436.30 |
|
|
|
| 8 |
B |
383 |
368 |
103.94 |
|
|
|
| 9 |
B |
219 |
210 |
375.17 |
|
|
|
Unscaled Zero Point Vibrational Energy (zpe) 5937.8 cm
-1
Scaled (by 0.9595) Zero Point Vibrational Energy (zpe) 5697.3 cm
-1
See section
III.C.1 List or set vibrational scaling factors
to change the scale factors used here.
See section
III.C.2
Calculate a vibrational scaling factor for a given set of molecules
to determine the least squares best scaling factor.
Geometric Data calculated at CCD/6-31G
Point Group is C2
Cartesians (Å)
| Atom |
x (Å) |
y (Å) |
z (Å) |
|---|
| Be1 |
0.000 |
0.000 |
0.005 |
| O2 |
0.000 |
1.414 |
-0.023 |
| O3 |
0.000 |
-1.414 |
-0.023 |
| H4 |
0.239 |
2.314 |
0.171 |
| H5 |
-0.239 |
-2.314 |
0.171 |
Atom - Atom Distances (Å)
| |
Be1 |
O2 |
O3 |
H4 |
H5 |
| Be1 | | 1.4140 | 1.4140 | 2.3324 | 2.3324 |
O2 | 1.4140 | | 2.8274 | 0.9517 | 3.7406 | O3 | 1.4140 | 2.8274 | | 3.7406 | 0.9517 | H4 | 2.3324 | 0.9517 | 3.7406 | | 4.6530 | H5 | 2.3324 | 3.7406 | 0.9517 | 4.6530 | |
 More geometry information
More geometry information
Calculated Bond Angles
| atom1 |
atom2 |
atom3 |
angle |
|
atom1 |
atom2 |
atom3 |
angle |
| Be1 |
O2 |
H4 |
160.380 |
|
Be1 |
O3 |
H5 |
160.380 |
| O2 |
Be1 |
O3 |
177.734 |
|
Electronic energy levels
Charges, Dipole, Quadrupole and Polarizability
Jump to
S1C1
S1C2
Energy calculated at CCD/6-31G
| | hartrees |
|---|
| Energy at 0K | -165.874474 |
| Energy at 298.15K | |
| HF Energy | -165.602766 |
| Nuclear repulsion energy | 49.177116 |
The energy at 298.15K was derived from the energy at 0K
and an integrated heat capacity that used the calculated vibrational frequencies.
Vibrational Frequencies calculated at CCD/6-31G
| Mode Number |
Symmetry |
Frequency
(cm-1) |
Scaled Frequency
(cm-1) |
IR Intensities
(km mol-1) |
Raman Act
(Å4/u) |
Dep P |
Dep U |
|---|
| 1 |
Σg |
4088 |
3923 |
0.00 |
|
|
|
| 2 |
Σg |
786 |
754 |
0.00 |
|
|
|
| 3 |
Σu |
4087 |
3921 |
348.11 |
|
|
|
| 4 |
Σu |
1670 |
1602 |
467.03 |
|
|
|
| 5 |
Πg |
171i |
165i |
0.00 |
|
|
|
| 5 |
Πg |
171i |
165i |
0.00 |
|
|
|
| 6 |
Πu |
383 |
367 |
43.82 |
|
|
|
| 6 |
Πu |
383 |
367 |
43.82 |
|
|
|
| 7 |
Πu |
187i |
179i |
616.18 |
|
|
|
| 7 |
Πu |
187i |
179i |
616.18 |
|
|
|
Unscaled Zero Point Vibrational Energy (zpe) 5339.7 cm
-1
Scaled (by 0.9595) Zero Point Vibrational Energy (zpe) 5123.5 cm
-1
See section
III.C.1 List or set vibrational scaling factors
to change the scale factors used here.
See section
III.C.2
Calculate a vibrational scaling factor for a given set of molecules
to determine the least squares best scaling factor.
Geometric Data calculated at CCD/6-31G
Point Group is D∞h
Cartesians (Å)
| Atom |
x (Å) |
y (Å) |
z (Å) |
|---|
| Be1 |
0.000 |
0.000 |
0.000 |
| O2 |
0.000 |
0.000 |
1.407 |
| O3 |
0.000 |
0.000 |
-1.407 |
| H4 |
0.000 |
0.000 |
2.357 |
| H5 |
0.000 |
0.000 |
-2.357 |
Atom - Atom Distances (Å)
| |
Be1 |
O2 |
O3 |
H4 |
H5 |
| Be1 | | 1.4072 | 1.4072 | 2.3566 | 2.3566 |
O2 | 1.4072 | | 2.8144 | 0.9494 | 3.7638 | O3 | 1.4072 | 2.8144 | | 3.7638 | 0.9494 | H4 | 2.3566 | 0.9494 | 3.7638 | | 4.7132 | H5 | 2.3566 | 3.7638 | 0.9494 | 4.7132 | |
 More geometry information
More geometry information
Calculated Bond Angles
| atom1 |
atom2 |
atom3 |
angle |
|
atom1 |
atom2 |
atom3 |
angle |
| Be1 |
O2 |
H4 |
180.000 |
|
Be1 |
O3 |
H5 |
180.000 |
| O2 |
Be1 |
O3 |
180.000 |
|
Electronic energy levels
Charges, Dipole, Quadrupole and Polarizability
